Achieving diffraction limited results using geometric ray tracing in Zemax poses a challenge that must be overcome to correctly model realistic systems.
Method For Laser Source Definition in ZEMAX To Enable Realistic Modelling With Raytracing
Alexander Brodsky and Natan Kaplan
HOLO/OR
Keywords: optical design, multi-mode lasers, partially coherent, BSDF, ZEMAX, beam quality factor, M2
Abstract
By default, optical systems are usually designed for single mode lasers. Nonetheless, many industrial lasers have M2 in the range from 3 to about 100 and are often called “multi-mode” or “partially coherent” lasers. Among those laser sources are multimode fiber lasers, multimode fiber coupled diode lasers, excimers, multimode solid-state lasers, and VCSEL arrays. While they have some disadvantages in terms of focus-ability, higher M2 lasers offer higher power than single mode lasers and require lower precision of optical elements in the system.
Unfortunately, Zemax™, one of the most common modelling software tools, does not offer a standard method for modelling multi-mode lasers in its sequential mode, thus compelling most designers to design for single-mode sources, and then try to account for the multi-mode effect by approximations. Even when designing for a single-mode laser, Ray-tracing tends to yield nonrealistic results in places of interest such as lens focal planes.
In this article we discuss a new method for simulating and optimizing both single and multi-mode lasers in Zemax™, by applying a scattering model. This concept allows one to use geometrical ray tracing to achieve physical-optics like results, including realistic spot size at lens foci, while still being fast and allowing for simple system optimization.
We first discuss the nature of lasers and the definition of M2. Afterwards we demonstrate our new scattering model method for ray tracing simulations and show the results. In the last section we present specific case studies to show the effectiveness and limits of the method.
1. Introduction
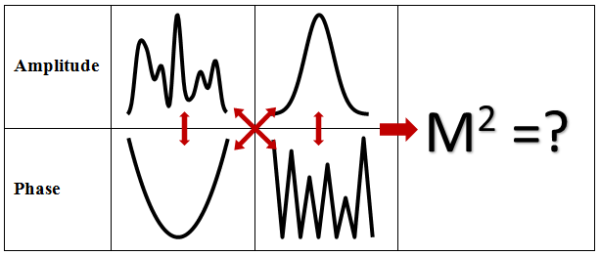
Any laser beam can be described by three parameters: wavelength, amplitude (or intensity) spatial distribution, and phase (or wavefront) spatial distribution. The unique property of a single-mode laser beam is a Gaussian amplitude and zero phase difference in the waist position. Multi-mode laser beams have arbitrary amplitude and phase.
Beam quality (or how “multi-mode” is the beam) of the laser beam is typically defined by the M2 term. This is a simplified number which takes into account all three laser parameters, and re-defines them in terms of beam size and beam divergence instead of amplitude and phase. In figure 1 we show a few examples of phase and amplitude profiles that statistically share the same M2.Assuming that the wavelength is constant, the M2 of the laser can be modified by changing the beam size and divergence.
To understand M2 better, let’s consider two cases: A single-mode Gaussian beam followed by negative ideal lens vs. an optical diffuser. In both cases beam divergence and diameter at waist can be equal, but for the first case we will say that beam kept being single-mode, and for the second case the beam became multi-mode. The explanation is that for the first case we can easily subtract the wave-front phase addition of the lens, by placing a positive lens, and the laser will return to be perfectly single mode. Mathematically we can do the same for the second example as well, but practically it’s much more complex to find the exact inverse wavefront phase that removes the diffuser effect.
So is the definition of a “multi-mode laser beam” related to just how easy it is to find an appropriate correction to convert it to a single-mode beam by utilizing previous knowledge about the laser beam? We would say yes – at least partially.
By using this insight, we can see that the general effects of M2 on an optical systems’ performance can be modeled by any wavefront phase addition that is “non-reconstructable” – i.e. does not share any symmetries with the optical components in the system.
Optical design tools have very good coverage for modeling and optimization using geometrical rays tracing. Physical optics has less developed tools and struggles with limitation of computers’ memory and time consumption. Thus, the optimal solution for modeling M2 is to find a way to use geometrical rays tracing kernel to solve problems associated with physical optics (e.g. complex wave presentation of light). In the next section we present a few ideas for doing so, based on the insight that the rays source should create rays distributions that are non-reconstructable.
2. Simulation modeling of multimode beams using geometrical rays tracing:
The basic idea is to apply a wavefront shape that is uncorrelated with all other optical parts within the optical system. For example, if all optical parts in the optical setup are prisms, then a multimode laser source can be modeled by applying a spherical wavefront. In a case where the optical setup is based on lenses, then for multi-mode laser one can use a wavefront with prismatic optical power, for example prisms array. Prism array, or lens array, are universal solutions that will be suitable for most of the laser systems, except for systems with multiple arrays. However, some standard optimization methods using arrays become insufficient, due to the complexity to control individual rays and limited geometry options. Therefore, arrays are not a good modeling option.
We are looking for a special wavefront with s geometry that can’t be described by cartesian or radial symmetries.
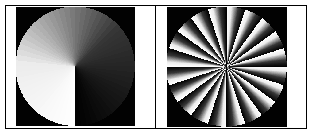
One option is using a wavefront with azimuthal symmetry. The most known example of which is Spiral Phase Plate (SPP) or Vortex [1],[2],[3]. This function is widely used for generation of Gaussian-Laguerre high modes. The M2 of the beam can be controlled by optical power of the SPP that appears as accumulated radians along azimuthal coordinates. In figure 2 shown SPP azimuthal wavefront with different optical power related to different M2 values.
This method has some similarity with skew rays’ method [4],[5]. Unlike skew rays, the azimuthal method has physical meaning, has no need for preliminary calculations and can be used with most analysis and optimization tools.
Another option, which is the method we use in this article, is to model the multi-mode effect by using BSDF [6],[7], type scattering. Originally, it was not created for this task, but by definition the scattering concept of redirected geometrical rays in a predefined configuration is uncorrelated with all other optical surfaces, making it suitable for use. This method was already used by Holo/Or to develop M2 transformation module, where anamorphic recombining of total M2 to two orthogonal coordinates is done [8],[9]. Furthermore, it was also confirmed experimentally [10]. In the examples we will concentrate on this scattering method.
3. Design Examples
3.1 Initial setup definitions in Zemax™
As in any laser optical system design, we start from defining general properties – Wavelength, Aperture Value, Appodization type, and Appodization factor.
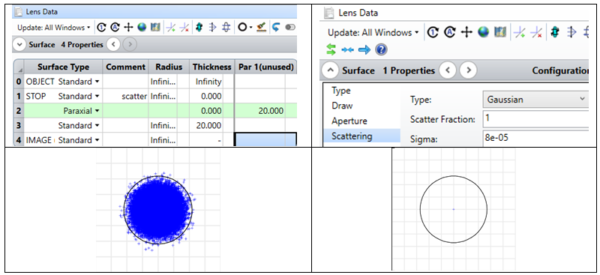
Appodization factor of Gaussian Appodization type is to be defined as 1, because later it will be used to adjust the divergence by scattering into the Airy disk. Next, insert a standard surface and in properties tab, choose scatter and then a specific scatter method to describe angular rays’ distribution and angles. In this paper we used Gaussian scatter type, set Scatter fraction to 1. After that open spot diagram and modify the scattering Sigma value, which is responsible for beam divergence, so that the rays in the spot diagram fill the Airy disk. This sigma value corresponds to single mode M2 =1.
To define a different M2 value, we multiply the Sigma value for M2=1 by the desired M2 value we want to model (for example we multiply sigma by a factor of 10 to model M2=10).
In figure 3 upper left we show Lens Data editor with simple setup including paraxial lens and interface of scattering window upper right. A spot diagram with divergence adjusted to fill the Airy disk is shown in figure 3 low left, and as reference a spot diagram without added scattering in the low right. We see that without scattering all rays go to a single geometrical point, and don’t describe the real spot size.
In the next section we review few case studies to show the correctness of the model and the benefits of using it.
3.2 Focusing single mode laser beam by paraxial lens for M2 1 and 10
Here and in the next examples we used the optical calculator from Holo/Or.
First, it’s important to show that the model is consistent with theoretical values. For this purpose we will compare the beam size at the waist and at Rayleigh length distance from the waist, with a known ratio of √2
Simulation parameters: wavelength 1064 nm, beam diameter 6 mm, EFL 20 mm, Appodization factor 4, Aperture size 12 mm.
In figure 4 we show a 2D intensity map in ZX plane to show the new focus spot size. White dash lines are theoretical spot size, and green dashed lines related to simulated spot size. The calculated differences between theoretical and simulated values for single-mode M2=1 (left image) and multi=mode M2=10 (right image) are less than 2 %, which is close enough for most applications.
| M2=1 (Gaussian Sigma 0.8e-05) | M2=10 (Gaussian Sigma 0.8e-04) |
3.3 Fiber coupling using standard triplet coupler
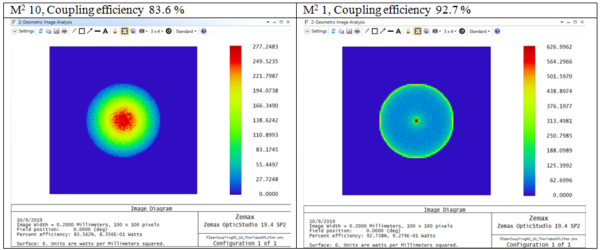
For fiber coupling efficiency analysis we chose a Triplet Collimator model from Thorlabs (TC25APC-1064 – 1060 nm, f=25.23 mm, NA=0.25, FC/APC). For the simulation we used the same incident beam of 6 mm diameter with M2=10 defined by scattering and wavelength 1064 nm. The task is to check coupling efficiency into fiber with NA 0.22 and core 0.1 mm. For position optimization we used the IMAE operand.
3.4 Comparison between Air spaced doublet and singlet for focusing
Highly multi-mode sources are less sensitive to optics quality, because optics imperfections are hidden by stronger beam quality optical effects. This knowledge can help economize investment in optics quality where it is not necessary.
In this example we continue with the same input parameters and compare a Thorlabs catalogue Air spaced doublet made of high refractive index glass (model ACA254-030-1064) with a simple plano-convex lens. Both focusing elements have an EFL 30 mm. Appodization factor was set as 2.25 which is typical for high power focusing applications to prevent aperture clipping.
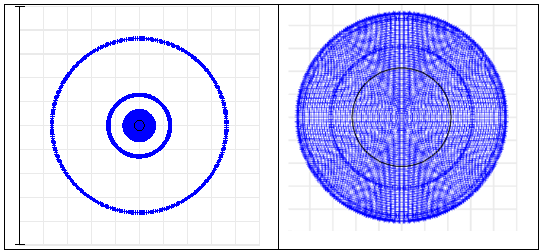
In figure 6 we show the spot diagram for a single-mode Gaussian source. Left picture is for singlet and right picture for doublet. Doublet performance is much better than singlet (less aberrations), based on the ray’s distribution relative to the Airy disk (black line circle).
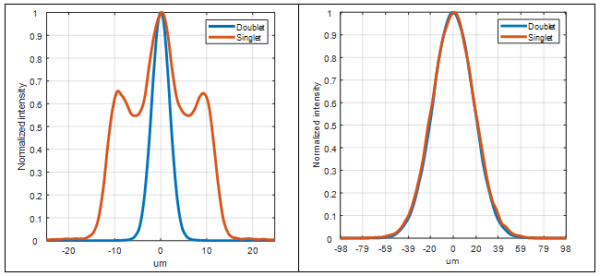
In the next figure 7 we show Geometrical image analysis for beam with M2=1 (left) and M2=10 (right).
For M2=1 the spot with the doublet looks nice and has only 20 % increase in spot size relative to the diffraction limit of the single-mode laser, but for the singlet lens the spot size is almost 4 times larger than the diffraction limit. For M2=10 the situation is totally different – doublet and singlet have identical results. In this specific case the price economy can reach few hundred dollars per setup, when using a multi-mode laser.
4. Summary and conclusions:
We presented a method to model real beams using geometrical rays tracing with additional angular scattering to get realistic beam size values along the entire optical path. The method is especially applicable for design of optical systems for multi-mode lasers. Being geometrical, our method has strong advantage in development time over the physical optics method and can be used for arbitrary multi-mode beams. The method has limitation, for cases where temporal coherence, interference and diffraction effects are important.
To show the power of the scattering method, we showed a few basic examples where the method was used for defocus analysis, fiber coupling efficiency estimation, and simulation of spot size and shape.
In most cases optics with more aberrations can be accepted for multi-mode lasers with high M2.
References:
1. Wang, Xuewen, et al. “Recent advances on optical vortex generation.” Nanophotonics 7.9 (2018): 1533-1556.
2. Tian, Ya-Li, et al. “Comparison of single-neutral-atom qubit between in bright trap and in dark trap.” Chinese Physics B 28.2 (2019): 023701.
3. Tiferet, Maor, et al. “Plasma dispersion effect based super-resolved imaging in silicon.” Nanoscale Imaging, Sensing, and Actuation for Biomedical Applications XVI. Vol. 10891. International Society for Optics and Photonics, 2019.
4. Zhang, Shuhe, Jinhua Zhou, and Lei Gong. “Skew line ray model of nonparaxial Gaussian beam.” Optics express 26.3 (2018): 3381-3393.
5. Colbourne, Paul D. “Generally astigmatic Gaussian beam representation and optimization using skew rays.” International Optical Design Conference. Optical Society of America, 2014.
6. Asmail, Clara. “Bidirectional scattering distribution function (BSDF): a systematized bibliography.” Journal of research of the National Institute of Standards and Technology 96.2 (1991): 215.
7. What scattering models are available in OpticStudio? https://my.zemax.com/en-US/Knowledge-Base/kb-article/?ka=KA-01415.
8. Brodsky, Alexander, and Natan Kaplan. “Analytical and practical implementation of anamorphic beam shaping in polar coordinates, Spinner system.” Optics & Laser Technology 107 (2018): 408-414.
9. LeanLine https://holoor.co.il/products/leanlinetm.
10. Brodsky, Alexander, and Natan Kaplan. “Experimental demonstration of anamorphic M 2 laser transformation in polar coordinates.” Optical Engineering 58.6 (2019): 065106.
11. Multimode fiber coupling https://my.zemax.com/en-US/Knowledge-Base/kb-article/?ka=KA-01351.
Subscribe to our newsletter
Fill in the form below and stay updated with the newest technologies, industry applications and upcoming events.