Hermite-Gauss mode conversion
Introduction
Arbitrary solutions of the paraxial Helmholtz equation can be expressed as combinations of Hermite-Gaussian modes (whose amplitude profiles are separable in x and y using Cartesian coordinates).
For many applications, it is useful to convert the fundamental laser mode TEM00 to a higher order of Hermite-Gaussian beams:
| Phase Element | Output Intensity | Phase Element | Output Intensity | ||
| TEM00 |  |  | TEM20 |  |  |
| TEM01 |  |  | TEM12 |  |  |
| TEM10 |  |  | TEM21 |  |  |
| TEM11 |  |  | TEM22 |  |  |
| TEM02 |  |  |
Each mode HGlm is denoted by two indices, l & m, which represent the number of modes in the x & y directions, respectively.
Typical Applications
- Communication
- Scientific & research
- Scanning applications
- STED microscopy
- Optical tweezing
- Optical trapping
Feature
- Aberration free
- High efficiency
Typical Optical set-up:

Typical Operating Principle
The operating principle is quite straight-forward – a Fourier Transform (FT) is applied on the initial field amplitude and phase to obtain the desired field (or intensity) at far-field. In this way, the fundamental Gaussian beam TEM_00 is converted to a higher order of Hermite-Gaussian modes. For example – conversion of TEM_00 to TEM_10:
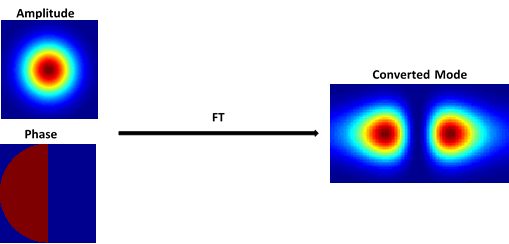
For the phase-plate element, the height of the step is defined as:
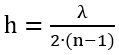
where n is the refractive index of the material.
Design Considerations:
For a high-quality performance, the laser output should be Single Mode (TEM00 with an M2 value <1.3. If the M2 is larger, it may still be possible to reduce the M2 value by inserting a spatial filter in between the laser and the DOE lens component.
All optics in the beam path should be of high quality, i.e. have a low irregularity figure, in order not to introdcue wav-front errors which would degrade the diffractive phase element’s performance.
General Specifications:
| Materials: | Fused Silica, Sapphire, ZnSe, Plastics |
| Wavelength range: | 193[nm] to 10.6[μm] |
| DOE design: | Binary (2-level) |
| Element size: | Few mm to 100 [mm] |
| Coating (optional): | AR/AR Coating |
| Custom Design: | Available |
π Phase-Plate
Introduction:
For many applications, it is necessary to use a phase element with a π-phase at the center. For imaging purposes using this element will result in an increased depth-of-focus, and for particle manipulation purpose, using this element will result in optical tweezing\trapping.
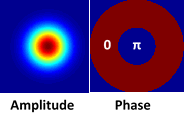
Standard Products:
| Part Number | Diameter [mm] | Aperture size [mm] | Material | Description | Add to Quote |
| PE-202 | 25.4 | 23.6 | Fused Silica | Half-space π difference mode converter, TEM01 (or TEM10) | Add to Quote |
| PE-230 | 25.4 | 23.6 | Fused Silica | Quarter-space π difference mode converter, TEM11 | Add to Quote |
| PE-215 | 11 | 9.2 | Fused Silica | Round π phase at the center, diameter 4817 μm | Add to Quote |
| PE-216 | 23.6 | 9.2 | Fused Silica | Round π phase at the center, diameter 5680 μm | Add to Quote |
| PE-217 | 20 | 23.6 | Fused Silica | Round π phase at the center, diameter 6200 μm | Add to Quote |
| PE-218 | 25.4 | 18.2 | Fused Silica | Round π phase at the center, diameter 8428 μm | Add to Quote |
| PE-219 | 25.4 | 23.6 | Fused Silica | Round π phase at the center, diameter 10838 μm | Add to Quote |
| PE-220 | 25.4 | 23.6 | Fused Silica | Round π phase at the center, diameter 7224 μm | Add to Quote |
| PE-221 | 11 | 9.2 | Fused Silica | Round π phase at the center, diameter 3612 μm | Add to Quote |
| PE-222 | 11 | 9.2 | Fused Silica | Round π phase at the center, diameter 4214 μm | Add to Quote |
| PE-223 | 11 | 9.2 | Fused Silica | Round π phase at the center, diameter 3000 μm | Add to Quote |
| PE-224 | 11 | 9.2 | Fused Silica | Round π phase at the center, diameter 5400 μm | Add to Quote |
| PE-225 | 25.4 | 23.6 | Fused Silica | Round π phase at the center, diameter 6384 μm | Add to Quote |
| PE-226 | 12.5 | 10.7 | Fused Silica | Round π phase at the center, diameter 6840 μm | Add to Quote |
| PE-227 | 25.4 | 23.6 | Fused Silica | Round π phase at the center, diameter 8900 μm | Add to Quote |
| PE-228 | 11 | 9.2 | Fused Silica | Round π phase at the center, diameter 1200 μm | Add to Quote |
| PE-229 | 11 | 9.2 | Fused Silica | Round π phase at the center, diameter 1800 μm | Add to Quote |
| PE-241 | 25.4 | 22.9 | Fused Silica | Round π phase at the center, diameter 3860 μm | Add to Quote |
For a quotation of an above Part Number, please specify the wavelength used.
Contact us for more information or for a custom solution.
References:
- Vortex lens application notes
- A novel vortex generator and mode converter for electrons
- Fluorescence microscopy with diffraction resolution barrier broken by stimulated emission
- A high frequency optical trap for atoms using Hermite-Gaussian beams
- Elegant Gaussian beams for enhanced optical manipulation
- Tunable cavity-enhanced photon pairs source in Hermite-Gaussian mode
- Near-field scattering of longitudinal fields
- Optical trapping of air-borne light-absorbing particles with various laser beams
- Optical trapping with π-phase cylindrical vector beams

